
Zadanie Konferencja - poprawka [A] (ko2)
Pomóż nam usprawnić bazę zadań!
Conference - Rectification [A]
Memory limit: 32 MB
You must have heard about Great Bitonic Conference (if not, read the description of the "Conference" task). Organizers of the GBC are in trouble again and they are seeking your help. The original version of the registration system has a special mechanism for maximizing the income from the conference. It is achieved by canceling some of the booked tickets (it allows to reduce expenses on the renting of conference rooms). Such an approach is not acceptable however. People are dissatisfied with the fact that conference's organizers cancelled some of the tickets booked within a single reservation. You are asked to modify the registration system in such way, that the income from the conference is maximized, while cancellation of only whole reservations is allowed.
Task
Write a program which:
- reads from the standard input the prices of tickets, the size of a room, the cost of renting a room and the list of reservations,
- calculates maximal profit from the conference, that can be obtained by potentially cancelling some of the reservations,
- writes the result to the standard output.
Input
In the first line of the standard input there are four integers: 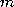 ,
, 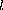 ,
,
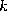 and
and  (
(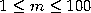 ,
, 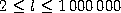 ,
, 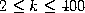 ,
,  ), separated by single spaces.
They represent: the number of presentations, the number of reservations,
the size of a single room and the cost of renting a single room. The second line contains
exactly
), separated by single spaces.
They represent: the number of presentations, the number of reservations,
the size of a single room and the cost of renting a single room. The second line contains
exactly 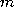 numbers
numbers 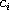 (
(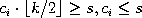 ),
separated by
single spaces (the lower limit on the value of
),
separated by
single spaces (the lower limit on the value of 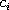 is due to profitability of renting a room for
is due to profitability of renting a room for 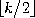 participants of a conference).
They represent prices of tickets for the presentations (numbered from
participants of a conference).
They represent prices of tickets for the presentations (numbered from 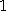 to
to 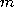 ).
Following
).
Following 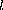 lines contain descriptions of reservations.
Each reservation is represented by two integers
lines contain descriptions of reservations.
Each reservation is represented by two integers
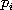 and
and 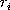 (
(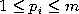 ,
, 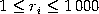 ), separated by a single space.
They represent the number of a presentation and the number of tickets booked for this presentation.
It is only allowed to cancel all tickets reserved within the same reservation.
), separated by a single space.
They represent the number of a presentation and the number of tickets booked for this presentation.
It is only allowed to cancel all tickets reserved within the same reservation.
Output
The first and only line of the standard output should contain exactly one integer - the total income that can be obtained by potentially cancelling only whole reservations.
Example
For the input data:
3 2 10 30 7 10 8 1 9 3 13
the correct result is:
77
Task author: Piotr Stanczyk.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English